java杨辉三角视频

A. javaSCRIPT输出杨辉三角

代码如下：

function print(v){

if (typeof v == "number") {

var w = 30;

if(n>30) w = (n-30) + 40;

var s = '<span style="padding:4px 2px;display:inline-block;text-align:center;width:' + w + 'px;">'+v+'</span>';

document.write(s);

}else{

document.write(v);

}

}

var n = prompt("请输入幂数：",9);

n = n - 0;

var t1 = new Date();

var a1 = [1,1];

var a2 = [1,1];

print('<div style=text-align:center;">');

for (var i = 0;i <=n;i++){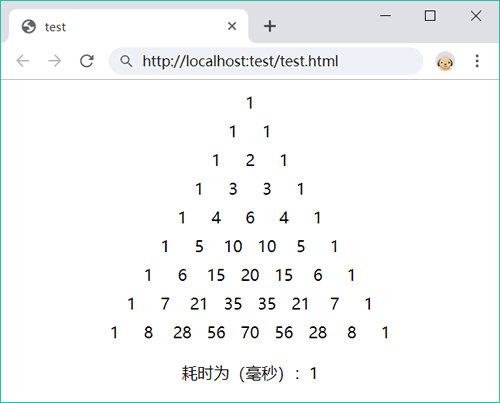

for (var j = 1; j < i + 2; j++) {

print(c(i,j));

}

print("<br />");

}

print("</div>");

var t2 = new Date();

print("<p style='text-align:center;'>耗时为（毫秒）："+(t2-t1)+"</p>");

function c(x,y){

if ((y == 1) || (y == x + 1)) return 1;

return c(x-1,y-1) + c(x-1,y);

}

(1)java杨辉三角视频扩展阅读

杨辉三角的特点：

1、每个数等于它上方两数之和。

2、每行数字左右对称，由1开始逐渐变大。

3、第n行的数字有n项。

4、前n行共[(1+n)n]/2 个数。

5、第n行的m个数可表示为C(n-1，m-1)，即为从n-1个不同元素中取m-1个元素的组合数。

6、第n行的第m个数和第n-m+1个数相等 ，为组合数性质之一。

7、每个数字等于上一行的左右两个数字之和。可用此性质写出整个杨辉三角。即第n+1行的第i个数等于第n行的第i-1个数和第i个数之和，这也是组合数的性质之一。

B. Java语言杨辉三角

打印杨辉三角代码如下：

public class woo {

public static void triangle(int n) {

int[][] array = new int[n][n];//三角形数组

for(int i=0;i<array.length;i++){

for(int j=0;j<=i;j++){

if(j==0||j==i){

array[i][j]=1;

}else{

array[i][j] = array[i-1][j-1]+array[i-1][j];

}

System.out.print(array[i][j]+" ");

}

System.out.println();

}

}

public static void main(String args[]) {

triangle(9);

}

}

(2)java杨辉三角视频扩展阅读：

杨辉三角起源于中国，在欧洲这个表叫做帕斯卡三角形。帕斯卡（1623----1662）是在1654年发现这一规律的，比杨辉要迟393年。它把二项式系数图形化，把组合数内在的一些代数性质直观地从图形中体现出来，是一种离散型的数与形的优美结合。

杨辉三角具有以下性质：

1、最外层的数字始终是1；

2、第二层是自然数列；

3、第三层是三角数列；

4、角数列相邻数字相加可得方数数列。

C. 用java编写金字塔型的杨辉三角形程序

import java.util.*;
class tt
{
public static void main(String[]args)
{
    Scanner sc=new Scanner(System.in);
    int n=sc.nextInt();
int[][] a=new int[n][n];
int i=0,j=0;
for(i=0;i<n;i++)
{
for(j=n;j>=i;j--)
System.out.print("	");
for(j=0;j<=i;j++)
{
if(i==j||j==0)
a[i][j]=1;
else
a[i][j]=a[i-1][j]+a[i-1][j-1];
System.out.print(a[i][j]+"		");
if(i==j)
System.out.println();
}
}
}
}